What the Intermediate Value Theorem 🥸ACTUALLY🥸 says! #apcalculus #apcalc #unit1 #shorts

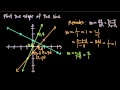
If we have a continuous function f within an interval x=a to x=b, and this function has a negative value at a and a positive value at b, it's guaranteed to cross the x-axis somewhere between a and b. This principle holds true regardless of the function's direction of change - whether it's increasing or decreasing within the interval.

So if f(a) less than 0 less than f(b) or f(a) greater than 0 greater than f(b), there must exist at least one point c within the interval a to b where f(c)=0. This is a powerful tool in calculus, offering a mathematical guarantee that continuous functions will hit every value in between their endpoints, thus ensuring an x-axis intersection within specified bounds.

#Calculus #IntermediateValueTheorem #ContinuousFunctions

Unit 1 of AP Calculus is all about Limits and Continuity:
1.1 Introducing Calculus: Can Change Occur at an Instant?
1.2 Defining Limits and Using Limit Notation
1.3 Estimating Limit Values from Graphs
1.4 Estimating Limit Values from Tables
1.5 Determining Limits Using Algebraic Properties of Limits
1.6 Determining Limits Using Algebraic Manipulation
1.7 Selecting Procedures for Determining Limits
1.8 Determining Limits Using the Squeeze Theorem
1.9 Connecting Multiple Representations of Limits
1.10 Exploring Types of Discontinuities
1.11 Defining Continuity at a Point
1.12 Confirming Continuity over an Interval
1.13 Removing Discontinuities
1.14 Connecting Infinite Limits and Vertical Asymptotes
1.15 Connecting Limits at Infinity and Horizontal Asymptotes
1.16 Working with the Intermediate Value Theorem (IVT)

_____

For extra help with your AP Calc (AB or BC), get my Ultimate Review Packet to help you review all year long and get prepared for the AP test:

AB: https://www.ultimatereviewpacket.com/courses/calculus-ab
BC: https://www.ultimatereviewpacket.com/courses/calculus-bc

Видео What the Intermediate Value Theorem 🥸ACTUALLY🥸 says! #apcalculus #apcalc #unit1 #shorts канала Krista King