Maps, Discrete Time Dynamical Systems - Introduction and Use
We introduce a new class of dynamical systems in which time is discrete, rather than continuous. These systems are known as difference equations, recursion relations, iterated maps, discrete maps or simply maps. Some phenomena are better modeled mathematically by discrete time maps, rather than differential equations. Maps are the more general class of dynamical system, since the numerical algorithms which solve differential equations are actually discrete time-step maps which are just a small subset of all possible maps. Other uses of maps are to simplify the study of phenomena that are otherwise complicated in a continuous setting.
We are focusing on maps because one-dimensional maps can show chaos, whereas differential equations, like the Lorenz equations, require three dimensions for chaos.
► Next, the logistic map, an example map with rich behavior
https://youtu.be/PVo1mHnU7WU
► Additional background
Lorenz map on strange attractor https://youtu.be/P4tjxOFnGNo
Lorenz equations introduction https://youtu.be/fIG2jtOhW0U
Definitions of chaos and attractor https://youtu.be/uDpYU01dhk0
Lyapunov exponents to quantify chaos https://youtu.be/22VVVn1zPdM
► Robert May's 1976 article introducing the logistic map (PDF)
https://is.gd/logisticmappaper
► From 'Nonlinear Dynamics and Chaos' (online course).
Playlist https://is.gd/NonlinearDynamics
► Dr. Shane Ross, Virginia Tech professor (Caltech PhD)
Subscribe https://is.gd/RossLabSubscribe
► Follow me on Twitter
https://twitter.com/RossDynamicsLab
► Course lecture notes (PDF)
https://is.gd/NonlinearDynamicsNotes
► Advanced lecture on maps from another course of mine
https://youtu.be/NYoA5B2qsdc
References:
Steven Strogatz, "Nonlinear Dynamics and Chaos", Chapter 10: One-Dimensional Maps
Poincare map largest Liapunov exponent fractal dimension of lorenz attractor box-counting dimension crumpled paper stable focus unstable focus supercritical subcritical topological equivalence genetic switch structural stability Andronov-Hopf Andronov-Poincare-Hopf small epsilon method of multiple scales two-timing Van der Pol Oscillator Duffing oscillator nonlinear oscillators nonlinear oscillation nerve cells driven current nonlinear circuit glycolysis biological chemical oscillation Liapunov gradient systems Conley index theory gradient system autonomous on the plane phase plane are introduced 2D ordinary differential equations cylinder bifurcation robustness fragility cusp unfolding perturbations structural stability emergence critical point critical slowing down supercritical bifurcation subcritical bifurcations buckling beam model change of stability nonlinear dynamics dynamical systems differential equations dimensions phase space Poincare Strogatz graphical method Fixed Point Equilibrium Equilibria Stability Stable Point Unstable Point Linear Stability Analysis Vector Field Two-Dimensional 2-dimensional Functions Hamiltonian Hamilton streamlines weather vortex dynamics point vortices topology Verhulst Oscillators Synchrony Torus friends on track roller racer dynamics on torus Lorenz equations chaotic strange attractor convection chaos chaotic
#NonlinearDynamics #DynamicalSystems #DifferenceEquation #PoincareMap #chaos #LorenzAttractor #LyapunovExponent #Lyapunov #Liapunov #Oscillators #Synchrony #Torus #Bifurcation #Hopf #HopfBifurcation #NonlinearOscillators #AveragingTheory #LimitCycle #Oscillations #nullclines #RelaxationOscillations #VanDerPol #VanDerPolOscillator #LimitCycles #VectorFields #topology #geometry #IndexTheory #EnergyConservation #Hamiltonian #Streamfunction #Streamlines #Vortex #SkewGradient #Gradient #PopulationBiology #FixedPoint #DifferentialEquations #SaddleNode #Eigenvalues #HyperbolicPoints #NonHyperbolicPoint #CuspBifurcation #CriticalPoint #buckling #PitchforkBifurcation #robust #StructuralStability #DifferentialEquations #dynamics #dimensions #PhaseSpace #PhasePortrait #PhasePlane #Poincare #Strogatz #Wiggins #Lorenz #VectorField #GraphicalMethod #FixedPoints #EquilibriumPoints #Stability #NonlinearODEs #StablePoint #UnstablePoint #Stability #LinearStability #LinearStabilityAnalysis #StabilityAnalysis #VectorField #TwoDimensional #Functions #PopulationGrowth #PopulationDynamics #Population #Logistic #GradientSystem #GradientVectorField #Cylinder #Pendulum #Newton #LawOfMotion #dynamics #Poincare #mathematicians #maths #mathsmemes #math4life #mathstudents #mathematician #mathfacts #mathskills #mathtricks #KAMtori #Hamiltonian
Видео Maps, Discrete Time Dynamical Systems - Introduction and Use автора The Science Behind Personality Types
Видео Maps, Discrete Time Dynamical Systems - Introduction and Use автора The Science Behind Personality Types
Информация
30 октября 2024 г. 13:33:45
00:10:56
Похожие видео
 Художньо-продуктивна діяльність.Аплікація
Художньо-продуктивна діяльність.Аплікація ZOZI ЛУЧШАЯ ЗАМЕНА летишопс РУССКИЙ КЕШБЭК СЕРВИС letyshops удаляем
ZOZI ЛУЧШАЯ ЗАМЕНА летишопс РУССКИЙ КЕШБЭК СЕРВИС letyshops удаляем 10-11-2024
10-11-2024 0-02-05-d25c769af008b1344775b6b6006f1eeed3f195f7fa49a5ae11617fed7c7b7372_6de5dae855066755
0-02-05-d25c769af008b1344775b6b6006f1eeed3f195f7fa49a5ae11617fed7c7b7372_6de5dae855066755 logout animation button #html#css#js#logout#button
logout animation button #html#css#js#logout#button Бесшовный Wi-Fi в частном доме (Mesh - сеть TP-Link Deco)
Бесшовный Wi-Fi в частном доме (Mesh - сеть TP-Link Deco) 10-11-2024
10-11-2024 VLOG-ИТОГ: новости и планы / хейтеры / прихожу в форму / новый канал II всё ещё не отошла II
VLOG-ИТОГ: новости и планы / хейтеры / прихожу в форму / новый канал II всё ещё не отошла II PXL_20241110_074206774
PXL_20241110_074206774 Методичний коучинг - 15.01.2015 року
Методичний коучинг - 15.01.2015 року Желаю вам успехов
Желаю вам успехов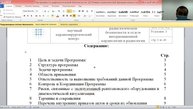 Введение по РБ Цель Структура по РБ
Введение по РБ Цель Структура по РБ Desktop 2024.11.10 - 10.44.55.07
Desktop 2024.11.10 - 10.44.55.07 Регрессия в прошлые жизни, Симферополь, ч1
Регрессия в прошлые жизни, Симферополь, ч1 Подсказка дня от МАК
Подсказка дня от МАК АгроРУСЬ 2011 - Молодежный межвузовский коллектив
АгроРУСЬ 2011 - Молодежный межвузовский коллектив Ещё пара слов о соматических упражнениях
Ещё пара слов о соматических упражнениях От образца к модели (вторая фаза) Движение к абстрактному Принцип параллелизма 2011
От образца к модели (вторая фаза) Движение к абстрактному Принцип параллелизма 2011 Как же всё таки убрать водяной знак в Alight Motion
Как же всё таки убрать водяной знак в Alight Motion How to Stop an ISFP from Abusive Behaviors | CS Joseph Responds
How to Stop an ISFP from Abusive Behaviors | CS Joseph Responds
