Spacetime geometry | Wikipedia audio article
This is an audio version of the Wikipedia Article:
https://en.wikipedia.org/wiki/Spacetime
00:03:17 1 Introduction
00:03:26 1.1 Definitions
00:09:28 1.2 History
00:19:46 2 Spacetime in special relativity
00:19:57 2.1 Spacetime interval
00:31:57 2.2 Reference frames
00:33:07 2.3 Light cone
00:33:39 2.4 Relativity of simultaneity
00:33:57 2.5 Invariant hyperbola
00:35:04 2.6 Time dilation and length contraction
00:35:25 2.7 Mutual time dilation and the twin paradox
00:35:46 2.7.1 Mutual time dilation
00:35:54 2.7.2 Twin paradox
00:36:35 2.8 Gravitation
00:39:22 3 Basic mathematics of spacetime
00:40:12 3.1 Galilean transformations
00:41:32 3.2 Relativistic composition of velocities
00:43:06 3.3 Time dilation and length contraction revisited
00:46:36 3.4 Lorentz transformations
00:49:02 3.4.1 Deriving the Lorentz transformations
00:49:53 3.4.2 Linearity of the Lorentz transformations
00:50:05 3.5 Doppler effect
00:53:38 3.5.1 Longitudinal Doppler effect
00:59:38 3.5.2 Transverse Doppler effect
01:00:35 3.6 Energy and momentum
01:00:46 3.6.1 Extending momentum to four dimensions
01:01:55 3.6.2 Momentum of light
01:03:43 3.6.3 Mass-energy relationship
01:03:55 3.6.4 Four-momentum
01:04:08 3.7 Conservation laws
01:04:59 3.7.1 Total momentum
01:05:44 3.7.2 Choice of reference frames
01:06:01 3.7.3 Energy and momentum conservation
01:06:50 4 Beyond the basics
01:07:08 4.1 Rapidity
01:07:19 4.2 4‑vectors
01:08:50 4.2.1 Definition of 4-vectors
01:09:03 4.2.2 Properties of 4-vectors
01:10:44 4.2.3 Examples of 4-vectors
01:11:04 4.2.4 4-vectors and physical law
01:13:26 4.3 Acceleration
01:13:54 4.3.1 Dewan–Beran–Bell spaceship paradox
01:14:48 4.3.2 Accelerated observer with horizon
01:19:25 5 Introduction to curved spacetime
01:19:54 5.1 Basic propositions
01:20:41 5.2 Curvature of time
01:22:40 5.3 Curvature of space
01:22:58 5.4 Sources of spacetime curvature
01:23:21 5.4.1 Energy-momentum
01:23:37 5.4.2 Pressure and stress
01:25:03 5.4.3 Experimental verification
01:26:21 5.4.3.1 • Active, passive, and inertial mass
01:27:03 5.4.3.2 • Pressure as a gravitational source
01:27:10 5.4.3.3 • Gravitomagnetism
01:27:20 6 Technical topics
01:27:54 6.1 Is spacetime really curved?
01:30:22 6.2 Riemannian geometry
01:31:14 6.3 Curved manifolds
01:34:37 6.4 Privileged character of 3+1 spacetime
01:34:46 7 See also
01:36:14 8 Notes
01:36:51 9 Additional details
01:37:38 10 References
01:38:29 11 Further reading
01:38:48 12 External links
01:39:28 γmv approaches mv, the classical term for momentum. Following this perspective, γm can be interpreted as a relativistic generalization of m. Einstein proposed that the relativistic mass of an object increases with velocity according to the formula mrel
01:40:08 mrelc
01:43:42 ±pc.
01:43:47 Four-momentum
01:45:36 Conservation laws
01:46:33 Total momentum
01:47:43 m2v2 collide to produce a single particle of conserved mass m
01:48:05 (m1v1 + m2v2)/(m1 + m2). The total momentum p
01:49:36 Choice of reference frames
01:50:43 Energy and momentum conservation
01:51:06 v − u, the momentum p'
01:51:35 0 both before and after collision. In the Newtonian analysis, conservation of mass dictates that m
01:52:36 mv, fail to behave properly under Lorentzian transformation. The linear transformation of velocities v'
01:55:48 4.12 MeV. Most of the energy is carried off by the near-zero-mass neutrino.
01:55:58 Beyond the basics
01:56:08 The topics in this section are of significantly greater technical difficulty than those in the preceding sections and are not essential for understanding Introduction to curved spacetime.
01:56:24 Rapidity
02:01:03 {\displaystyle \beta
02:05:48 4‑vectors
02:07:23 Definition of 4-vectors
02:09:43 Properties of 4-vectors
02:14:16 Examples of 4-vectors
02:22:07 4-vectors and physical law
02:23:16 Acceleration
02:24:24 Dewan–Beran–Bell spaceship paradox
02:30:29 Accelerated observer with horizon
02:33:42 {\displaystyle \gamma
02:37:09 Introduction to curved spacetime
02:37:20 Basic propositions
02:41:29 GMmg /r2
02:42:47 Curvature of time
02:44:12 (2gh)1/2, so that its total energy E, as measured by an observer on the ground, is m + ½mv2/c2
02:44:55 m', since otherwise one would be able to construct a perpetual motion device. We therefore predict that E'
02:49:32 Curvature of space
02:57:32 Sources of spacetime curvature
02:59:40 j terms (green) represent isotropic pressure, and the i ≠ j terms (blue) represent shear stresses.One important conclusion to be derived from the equations is that, colloquially speaking, gravity itself creates gravity. Energy has mass. Even in Newtonian gravity, the gravitational field is associated with an energy, E
03:00:52 Energy-momentum
03:03:02 Pressure and stress
03:04:29 Experimental verification
03:05:33 • Active, passive, and inertial mass
03:08:31 • Pressure as a gravitational source
03:10:49 9, while bromine has Z
03:12:11 • Gravitomagnetism
03:14:02 Technical topics
03:14:12 Is spacetime ...
Видео Spacetime geometry | Wikipedia audio article автора Растительный музей
Видео Spacetime geometry | Wikipedia audio article автора Растительный музей
Информация
18 апреля 2024 г. 19:33:31
03:27:38
Похожие видео
 Nick Vujicic - Что-то большее
Nick Vujicic - Что-то большее 09:30 Плющ Павел 0-3 Хамурда Виталий стол 4 ЮГ-1 19.04.22
09:30 Плющ Павел 0-3 Хамурда Виталий стол 4 ЮГ-1 19.04.22 Цветение клубники 24.05.2020.
Цветение клубники 24.05.2020. XXI Finał WOŚP w Peterborough - Laima Grinenko
XXI Finał WOŚP w Peterborough - Laima Grinenko Молниеносный запуск локального сервера.
Молниеносный запуск локального сервера. 20.001. Nested Functions
20.001. Nested Functions![Master Any Language with ChatGPT Boost Your Language Skills [ru]](http://pic.rutubelist.ru/video/2025-05-09/8f/ea/8fea3e0357a1ff30c18c165761c0b216.jpg?size=s) Master Any Language with ChatGPT Boost Your Language Skills [ru]
Master Any Language with ChatGPT Boost Your Language Skills [ru] Wider Word 2 Student's book стр. 75 упр. 7 с субтитрами
Wider Word 2 Student's book стр. 75 упр. 7 с субтитрами Лейсан
Лейсан ЛЮБВИ МОЖНО НАУЧИТСЯ. Александр Хакимов.
ЛЮБВИ МОЖНО НАУЧИТСЯ. Александр Хакимов. Сеянцы хост, цель и трудности ее достижения
Сеянцы хост, цель и трудности ее достижения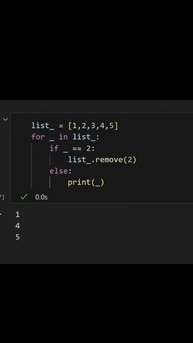 Никогда не делай так! Нельзя изменять итерируемый объект во время обхода! Почему
Никогда не делай так! Нельзя изменять итерируемый объект во время обхода! Почему отвечаю на вопросы 07.01.2020
отвечаю на вопросы 07.01.2020 Детские мультики свинка Пеппа бассейн плавать пепа
Детские мультики свинка Пеппа бассейн плавать пепа Подводный камень Resources в Unity
Подводный камень Resources в Unity Revan roil
Revan roil Недооцененный slice. Как его использовать и в каких случаях он вам пригодится в Python
Недооцененный slice. Как его использовать и в каких случаях он вам пригодится в Python 20.004. The Fn Trait Hierarchy
20.004. The Fn Trait Hierarchy Секрет супербыстрой сортировки itemgetter vs lambda! До 50% быстрее на больших данных
Секрет супербыстрой сортировки itemgetter vs lambda! До 50% быстрее на больших данных 12_загадок,_которые_не_может_решить_весь_интернет_А_ты_сможешь?
12_загадок,_которые_не_может_решить_весь_интернет_А_ты_сможешь?
