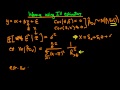Heteroskedasticity summary

This video provides an overview of what is meant by 'heteroskedastic errors' in econometrics.
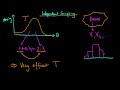
Hi there, in this video I am going to be talking about homoskedasticity as one of the Gauss-Markov assumptions. So, first of all, what do we mean by homoskedasticity? Well, in fact we mean homoskedasticity of our errors. Which means that the variance of our errors, given our independent variables 'x', is constant. So, if I was to think about there being some relationship between y and x, and I had some sort of sample of data, which looks something like this, and perhaps I then fit a straight line to this data so that I am using a linear model - linear in my independent variable 'x'. Then we can sort of think about the errors which our model is making are basically constant across our independent variable 'x'. They are basically the same as I increase my 'x' variable - all the errors lie within straight error bars. Well, we can contrast this with the situation where we have heteroskedastic errors. So here it would be the case if I had my y and x, and I had some points, some data points which as x increases there is a larger variance in y, if I then go ahead and fit a straight line to that data - so perhaps my straight line would do something like that. We can see that the errors which our model is making, are increasing in magnitude, as 'x' increases. So, if I fit an error line indicating the direction of increase of my errors, then you can see that my errors are increasing along my 'x' variable. So, this is what we call heteroskedasticity, so homo- in this context means that the errors are the same, so that's this sort of case, and hetero here means that the errors are different. Well, mathematically how do we write that? We write that the variance of our errors 'u' given our 'x', is some sort of function of x - it depends on 'x'. Here it is some sort of positive function because as my x increases, the magnitude of my errors increase as well. So, why do we care about our errors being homoskedastic? Well, as I said it is one of the Gauss-Markov assumptions, and if it is violated this means that our least-squared estimators are no longer BLUE. In particular, they are no longer best. So, there are other linear, unbiased estimators which have a lower sampling variance. Intuitively this means that there are other estimators which are linear and unbiased, which more often, or more frequently than least-squares will get closer to the true population parameters. And the intuition from this is essentially that - if I have heteroskedastic errors, there is some sort of information which is inherent in my system which I'm not including in my model. And perhaps if I include that information into my model, so I include the fact that I expect my errors to increase as 'x' increases, then perhaps I can come up with an estimator which actually gets closer to my y values more of the time. So that is the underlying intuition for why heteroskedasticity means that I can construct another estimator, which has a lower variance than least-squares. In the next few videos I'm going to give some actual examples of where heteroskedasticity arises, and that's going to conclude our discussion of the Gauss-Markov assumptions. Check out https://ben-lambert.com/econometrics-course-problem-sets-and-data/ for course materials, and information regarding updates on each of the courses. Quite excitingly (for me at least), I am about to publish a whole series of new videos on Bayesian statistics on youtube. See here for information: https://ben-lambert.com/bayesian/ Accompanying this series, there will be a book: https://www.amazon.co.uk/gp/product/1473916364/ref=pe_3140701_247401851_em_1p_0_ti

Видео Heteroskedasticity summary канала Ben Lambert