Continued Fractions 1: Introduction and Basic Examples - LearnMathsFree
SUPPORT ME ON PATREON! Click here: https://www.patreon.com/crystalmath
---
This is the first part in a video series about continued fractions. In this video, we define a finite continued fraction and explore some basic examples. More to follow.
Continued fractions are believed to have first appeared around 300 BC, in Euclid's Elements. A continued fraction is a sequence of integers arranged in a "nested fraction" format: that is, it is an expression obtained by writing a number as the sum of a number plus the reciprocal of another number, then writing *that* number as a number plus the reciprocal of another number, and so on. In this way, one obtains a sequence of numbers, written [a_0, a_1, ..., a_n] in the case of a finite continued fraction (which converges to some rational number), or [a_0, a_1, ... ] in the case of an infinite continued fraction (which can converge to any real number).
The aim of this series is to apply continued fractions in a number of contexts, most notably, to the solution of Pell's equation, x^2 - dy^2 = 1 (where d is square-free), and as a corollary, to solve equations of the form x^2 + dy^2 = k, where d may be positive or negative.
Video URL: https://youtu.be/R5HhNmFPLPQ
Channel URL: https://www.youtube.com/channel/UCtTFrEPIqaKfWyGkBi9Rmvg
Видео Continued Fractions 1: Introduction and Basic Examples - LearnMathsFree канала CrystalMath
---
This is the first part in a video series about continued fractions. In this video, we define a finite continued fraction and explore some basic examples. More to follow.
Continued fractions are believed to have first appeared around 300 BC, in Euclid's Elements. A continued fraction is a sequence of integers arranged in a "nested fraction" format: that is, it is an expression obtained by writing a number as the sum of a number plus the reciprocal of another number, then writing *that* number as a number plus the reciprocal of another number, and so on. In this way, one obtains a sequence of numbers, written [a_0, a_1, ..., a_n] in the case of a finite continued fraction (which converges to some rational number), or [a_0, a_1, ... ] in the case of an infinite continued fraction (which can converge to any real number).
The aim of this series is to apply continued fractions in a number of contexts, most notably, to the solution of Pell's equation, x^2 - dy^2 = 1 (where d is square-free), and as a corollary, to solve equations of the form x^2 + dy^2 = k, where d may be positive or negative.
Video URL: https://youtu.be/R5HhNmFPLPQ
Channel URL: https://www.youtube.com/channel/UCtTFrEPIqaKfWyGkBi9Rmvg
Видео Continued Fractions 1: Introduction and Basic Examples - LearnMathsFree канала CrystalMath
Показать
Комментарии отсутствуют
Информация о видео
Другие видео канала
 Continued Fractions 2 - Infinite Continued Fractions - LearnMathsFree
Continued Fractions 2 - Infinite Continued Fractions - LearnMathsFree Sequences 6: Continued Fraction
Sequences 6: Continued Fraction Infinite Continued Fractions, simple or not?
Infinite Continued Fractions, simple or not? Infinite fractions and the most irrational number
Infinite fractions and the most irrational number Infinite Fractions - Numberphile
Infinite Fractions - Numberphile Algorithm and Continued Fraction
Algorithm and Continued Fraction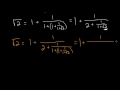 Continued Fractions: Square Root of 2
Continued Fractions: Square Root of 2![[ANT08] Continued fractions, Pell's equation, and units of Z[√d]](https://i.ytimg.com/vi/3ls3z-UzOSw/default.jpg) [ANT08] Continued fractions, Pell's equation, and units of Z[√d]
[ANT08] Continued fractions, Pell's equation, and units of Z[√d] Continued Fractions #3: Quickly Finding Continued Fractions of Rational Numbers
Continued Fractions #3: Quickly Finding Continued Fractions of Rational Numbers Continued Fractions - Professor John Barrow
Continued Fractions - Professor John Barrow Continued Fraction Trick | Simplification | वितत भिन्न | Maths | SSC/Bank/Railway/other exams
Continued Fraction Trick | Simplification | वितत भिन्न | Maths | SSC/Bank/Railway/other exams Vladimir I. Arnold - Continued fractions of quadratic irrationals (May 2007 lecture)
Vladimir I. Arnold - Continued fractions of quadratic irrationals (May 2007 lecture) Contour Integration #8 - Integral of sqrt(x)/(x^2 + 6x + 8)
Contour Integration #8 - Integral of sqrt(x)/(x^2 + 6x + 8) लंगड़ा भिन्न (Continued Fraction) Part-1 Simplification Math Trick for Rly/SSC/Bank By Kapildeo Sir
लंगड़ा भिन्न (Continued Fraction) Part-1 Simplification Math Trick for Rly/SSC/Bank By Kapildeo Sir Proof of Euler's Integral Formula (Gamma Function)
Proof of Euler's Integral Formula (Gamma Function) Intro to Continued Fractions
Intro to Continued Fractions Euler's infinite pi formula generator
Euler's infinite pi formula generator The Mandelbrot Set - The only video you need to see!
The Mandelbrot Set - The only video you need to see! Math Olympiad Lecture 10: Continued Fractions
Math Olympiad Lecture 10: Continued Fractions Continued Fractions #4: Continued Fraction of sqrt(n) (General Method)
Continued Fractions #4: Continued Fraction of sqrt(n) (General Method)