#Graph #BFS #Python | Min Reorder to Make All Cities Reach City 0 | Tree Traversal & Direction Fix
🚀 Problem Overview
We are given n cities numbered from 0 to n-1, forming a tree structure with exactly n-1 roads. However, the roads are directed, meaning we can only travel in one direction as defined in connections.
Our task is to reorient the minimum number of roads so that every city can reach city 0. It is guaranteed that reordering the roads can achieve this.
🛠️ Approach: BFS (Breadth-First Search)
To efficiently solve this problem, we use BFS (Breadth-First Search) with an undirected graph representation while keeping track of original road directions.
📝 Steps to Solve the Problem
1️⃣ Build an Undirected Graph Representation:
Convert the directed edges into a bidirectional adjacency list.
Store the original directed edges in a set, so we can check which edges need reordering.
2️⃣ Perform BFS Traversal:
Start from city 0 since it's the target destination.
Traverse its neighboring cities using BFS.
If a city has a road going outward (i.e., away from city 0), we increase the reorder count because we need to reverse that direction.
3️⃣ Count the Reordering Operations:
If the road (current → neighbor) exists in the original edge set, it means the direction is wrong, so we increment the reorder count.
Push the unvisited neighbors into the BFS queue and mark them visited.
4️⃣ Return the Final Count:
After traversing all nodes, we return the minimum number of roads that must be reversed.
🖥️ Code Implementation (BFS Approach in Python)
from collections import defaultdict, deque
class Solution:
def minReorder(self, n, connections):
graph = defaultdict(list)
original_edges = set()
# Step 1: Build the bidirectional graph and store original edges
for a, b in connections:
graph[a].append(b)
graph[b].append(a)
original_edges.add((a, b)) # Store original direction
visited = set()
queue = deque([0]) # Start BFS from city 0
changes = 0
# Step 2: BFS traversal
while queue:
city = queue.popleft()
visited.add(city)
for neighbor in graph[city]:
if neighbor not in visited:
if (city, neighbor) in original_edges:
changes += 1 # This edge needs reordering
queue.append(neighbor)
return changes
🔍 Complexity Analysis
Complexity Explanation
Time Complexity: O(n) Since we traverse each edge once, the time complexity is O(n-1) ≈ O(n).
Space Complexity: O(n) We store the graph in an adjacency list and a set, which takes O(n) space.
🛠️ Example Walkthrough
Example 1
🔹 Input:
n = 6
connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
🔹 Graph Representation:
0 ← 1 → 3 ← 2
↑
4 → 5
🔹 Required Reorientations:
Reverse (1 → 3) ✅
Reverse (2 → 3) ✅
Reverse (4 → 5) ✅
🔹 Output:
3
Example 2
🔹 Input:
n = 5
connections = [[1,0],[1,2],[3,2],[3,4]]
🔹 Graph Representation:
0 ← 1 → 2 ← 3 → 4
🔹 Required Reorientations:
Reverse (1 → 2) ✅
Reverse (3 → 4) ✅
🔹 Output:
2
📌 Key Takeaways
✅ The problem is solved using Graph Traversal (BFS/DFS).
✅ We track original edges and count wrong-direction edges.
✅ BFS ensures an efficient O(n) traversal.
✅ The approach guarantees minimum reordering needed.
Видео #Graph #BFS #Python | Min Reorder to Make All Cities Reach City 0 | Tree Traversal & Direction Fix канала CodeVisium
We are given n cities numbered from 0 to n-1, forming a tree structure with exactly n-1 roads. However, the roads are directed, meaning we can only travel in one direction as defined in connections.
Our task is to reorient the minimum number of roads so that every city can reach city 0. It is guaranteed that reordering the roads can achieve this.
🛠️ Approach: BFS (Breadth-First Search)
To efficiently solve this problem, we use BFS (Breadth-First Search) with an undirected graph representation while keeping track of original road directions.
📝 Steps to Solve the Problem
1️⃣ Build an Undirected Graph Representation:
Convert the directed edges into a bidirectional adjacency list.
Store the original directed edges in a set, so we can check which edges need reordering.
2️⃣ Perform BFS Traversal:
Start from city 0 since it's the target destination.
Traverse its neighboring cities using BFS.
If a city has a road going outward (i.e., away from city 0), we increase the reorder count because we need to reverse that direction.
3️⃣ Count the Reordering Operations:
If the road (current → neighbor) exists in the original edge set, it means the direction is wrong, so we increment the reorder count.
Push the unvisited neighbors into the BFS queue and mark them visited.
4️⃣ Return the Final Count:
After traversing all nodes, we return the minimum number of roads that must be reversed.
🖥️ Code Implementation (BFS Approach in Python)
from collections import defaultdict, deque
class Solution:
def minReorder(self, n, connections):
graph = defaultdict(list)
original_edges = set()
# Step 1: Build the bidirectional graph and store original edges
for a, b in connections:
graph[a].append(b)
graph[b].append(a)
original_edges.add((a, b)) # Store original direction
visited = set()
queue = deque([0]) # Start BFS from city 0
changes = 0
# Step 2: BFS traversal
while queue:
city = queue.popleft()
visited.add(city)
for neighbor in graph[city]:
if neighbor not in visited:
if (city, neighbor) in original_edges:
changes += 1 # This edge needs reordering
queue.append(neighbor)
return changes
🔍 Complexity Analysis
Complexity Explanation
Time Complexity: O(n) Since we traverse each edge once, the time complexity is O(n-1) ≈ O(n).
Space Complexity: O(n) We store the graph in an adjacency list and a set, which takes O(n) space.
🛠️ Example Walkthrough
Example 1
🔹 Input:
n = 6
connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
🔹 Graph Representation:
0 ← 1 → 3 ← 2
↑
4 → 5
🔹 Required Reorientations:
Reverse (1 → 3) ✅
Reverse (2 → 3) ✅
Reverse (4 → 5) ✅
🔹 Output:
3
Example 2
🔹 Input:
n = 5
connections = [[1,0],[1,2],[3,2],[3,4]]
🔹 Graph Representation:
0 ← 1 → 2 ← 3 → 4
🔹 Required Reorientations:
Reverse (1 → 2) ✅
Reverse (3 → 4) ✅
🔹 Output:
2
📌 Key Takeaways
✅ The problem is solved using Graph Traversal (BFS/DFS).
✅ We track original edges and count wrong-direction edges.
✅ BFS ensures an efficient O(n) traversal.
✅ The approach guarantees minimum reordering needed.
Видео #Graph #BFS #Python | Min Reorder to Make All Cities Reach City 0 | Tree Traversal & Direction Fix канала CodeVisium
Комментарии отсутствуют
Информация о видео
21 марта 2025 г. 10:35:08
00:00:10
Другие видео канала
 Strict Superset Checker – Detailed vs One-Liner Version #Python #Sets #Superset #Validation #Hacker
Strict Superset Checker – Detailed vs One-Liner Version #Python #Sets #Superset #Validation #Hacker Kids With the Greatest Candies 🍬 | Leetcode 75 Explained Python Solution #leetcode #python #coding
Kids With the Greatest Candies 🍬 | Leetcode 75 Explained Python Solution #leetcode #python #coding 🚀 Nearest Exit in a Maze using BFS | Optimal Python Solution 🔥 | #LeetCode75 #BFS #ShortestPath
🚀 Nearest Exit in a Maze using BFS | Optimal Python Solution 🔥 | #LeetCode75 #BFS #ShortestPath Product of Array Except Self in Python | Optimal O(n) Solution Without Division #Python #LeetCode
Product of Array Except Self in Python | Optimal O(n) Solution Without Division #Python #LeetCode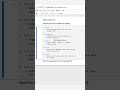 Master Sublime Text: 5 Essential Shortcuts for Efficient Text Editing #SublimeText #CodingEfficiency
Master Sublime Text: 5 Essential Shortcuts for Efficient Text Editing #SublimeText #CodingEfficiency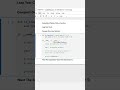 Leap Year Check – One-Liner Version #Python #HackerRank #LeapYear
Leap Year Check – One-Liner Version #Python #HackerRank #LeapYear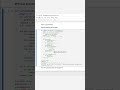 Python – Course Schedule: DFS Cycle Detection Approach (DSA) 🚀 #CourseSchedule #PythonDSA #GraphAlg
Python – Course Schedule: DFS Cycle Detection Approach (DSA) 🚀 #CourseSchedule #PythonDSA #GraphAlg Alphabet Rangoli – One-Liner Version #Python #HackerRank #OneLiner #PatternPrinting #AlphabetRangoli
Alphabet Rangoli – One-Liner Version #Python #HackerRank #OneLiner #PatternPrinting #AlphabetRangoli 🚀 Min Flips for Bitwise OR Equality | Python XOR/Bitwise Solution | LeetCode75 #BitManipulation
🚀 Min Flips for Bitwise OR Equality | Python XOR/Bitwise Solution | LeetCode75 #BitManipulation Go Armstrong Number Check: Long & One-Liner Approach #Go #Armstrong #CodingShorties #CodeVisium
Go Armstrong Number Check: Long & One-Liner Approach #Go #Armstrong #CodingShorties #CodeVisium Low-Code/No-Code Magic: Democratizing App Development #LowCode #NoCode #AppDev
Low-Code/No-Code Magic: Democratizing App Development #LowCode #NoCode #AppDev Master Confluence: 5 Essential Shortcuts for Efficient Team Documentation #Confluence #Documentation
Master Confluence: 5 Essential Shortcuts for Efficient Team Documentation #Confluence #Documentation Average of Distinct Heights – One-Liner Version #HackerRank #OneLiner #Sets #AverageCalculation
Average of Distinct Heights – One-Liner Version #HackerRank #OneLiner #Sets #AverageCalculation Python – Minimum Window Substring (Sliding Window Approach) 🚀 #PythonDSA #CodingInterview
Python – Minimum Window Substring (Sliding Window Approach) 🚀 #PythonDSA #CodingInterview ⚡ SQL One-Liner: Sample 10% of Rows Instantly! #SQL #DataScience #DataSampling
⚡ SQL One-Liner: Sample 10% of Rows Instantly! #SQL #DataScience #DataSampling #HackerRank #ShoeShopChallenge – Compact One-Liner Version: collections.Counter Shoe Shop Problem
#HackerRank #ShoeShopChallenge – Compact One-Liner Version: collections.Counter Shoe Shop Problem Underrated AI Tools for Education & Learning | #EdTech #AI #Learning
Underrated AI Tools for Education & Learning | #EdTech #AI #Learning 🔥 Rearrange Linked List: Odd-Even Index Grouping in O(n) Time & O(1) Space! 🚀 #Python #LeetCode75
🔥 Rearrange Linked List: Odd-Even Index Grouping in O(n) Time & O(1) Space! 🚀 #Python #LeetCode75 🚀 Path Sum III | Binary Tree | DFS Brute Force | LeetCode 75 Solution 🔥 #LeetCode #Python #Binary
🚀 Path Sum III | Binary Tree | DFS Brute Force | LeetCode 75 Solution 🔥 #LeetCode #Python #Binary Deep Dive: Probability Theorems & Laws for Data Science | #DataScience #Probability #MathTheorems
Deep Dive: Probability Theorems & Laws for Data Science | #DataScience #Probability #MathTheorems