IOE 2079 Baishakh Engineering Mathematics-1 Old is Gold Solution | Part-1 | Er. Brijkishor Jaiswal
IOE 2079 Baishakh Engineering Mathematics-1 Old is Gold Solution | Part-1 | Er. Brijkishor Jaiswal
Pdf solution: https://drive.google.com/file/d/1rV5Q-J4ddVfknXwhRQ-t7eLNDpuierw3/view?usp=sharing
IOE Old is Gold Question Collection: https://drive.google.com/file/d/1-z-1mHCy6jVw6ZBvdsrAV0I-Cbfs-QWz/view?usp=sharing
Questions Discussed:
01:52 1. State Leibnitz’s theorem. If \( y = \log(x + \sqrt{a^2 + x^2}) \) then using the theorem show that
\((a^2 + x^2)y_2 + xy_1 = 0\) and hence show that
\((a^2 + x^2)y_{n+2} + (2n+1)xy_{n+1} + n^2 y_n = 0\).
**[1+4]**
14:26 2. Assuming the validity of expansion, find the expansion of: \(\log(\sec x)\) by using Maclaurin’s theorem.
**[5]**
23:00 3. What do you mean by indeterminate form? State various forms of indeterminacy. Evaluate
\[
\lim_{x \to 0} \left(\frac{\sin x}{x}\right)^x
\]
**[5]**
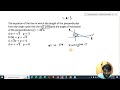
33:11 4. Define asymptotes and its types. Find the asymptotes of the curve
\[
x^3 + 4x^2y + 5xy^2 + 2y^3 + 2x + 4xy + 2y^2 - x - 9y + 1 = 0.
\]
**[1+4]**
This lecture is owned by Super Hundred Entrancepedia Institute. Any copy, download, reupload on social media platforms, or sharing with anyone is strictly prohibited.
website: https://entrancepedia.com/
Call/WhatsApp: +977 9742466664, 9813390297
Email: admission.super100class@gmail.com
Telegram Group: https://t.me/IOEAspirants_SHEI
Facebook Page: https://www.facebook.com/SuperHundredEntrancepedia
Facebook Group: fb://group/1011071599252168?ref=share
Видео IOE 2079 Baishakh Engineering Mathematics-1 Old is Gold Solution | Part-1 | Er. Brijkishor Jaiswal канала Super Hundred Entrancepedia Institute
Pdf solution: https://drive.google.com/file/d/1rV5Q-J4ddVfknXwhRQ-t7eLNDpuierw3/view?usp=sharing
IOE Old is Gold Question Collection: https://drive.google.com/file/d/1-z-1mHCy6jVw6ZBvdsrAV0I-Cbfs-QWz/view?usp=sharing
Questions Discussed:
01:52 1. State Leibnitz’s theorem. If \( y = \log(x + \sqrt{a^2 + x^2}) \) then using the theorem show that
\((a^2 + x^2)y_2 + xy_1 = 0\) and hence show that
\((a^2 + x^2)y_{n+2} + (2n+1)xy_{n+1} + n^2 y_n = 0\).
**[1+4]**
14:26 2. Assuming the validity of expansion, find the expansion of: \(\log(\sec x)\) by using Maclaurin’s theorem.
**[5]**
23:00 3. What do you mean by indeterminate form? State various forms of indeterminacy. Evaluate
\[
\lim_{x \to 0} \left(\frac{\sin x}{x}\right)^x
\]
**[5]**
33:11 4. Define asymptotes and its types. Find the asymptotes of the curve
\[
x^3 + 4x^2y + 5xy^2 + 2y^3 + 2x + 4xy + 2y^2 - x - 9y + 1 = 0.
\]
**[1+4]**
This lecture is owned by Super Hundred Entrancepedia Institute. Any copy, download, reupload on social media platforms, or sharing with anyone is strictly prohibited.
website: https://entrancepedia.com/
Call/WhatsApp: +977 9742466664, 9813390297
Email: admission.super100class@gmail.com
Telegram Group: https://t.me/IOEAspirants_SHEI
Facebook Page: https://www.facebook.com/SuperHundredEntrancepedia
Facebook Group: fb://group/1011071599252168?ref=share
Видео IOE 2079 Baishakh Engineering Mathematics-1 Old is Gold Solution | Part-1 | Er. Brijkishor Jaiswal канала Super Hundred Entrancepedia Institute
EntrancePedia ioe entrance preparation super-100 class online class for ioe entrance super hundred entrancepedia institute super100class brijkishor sir class IOE 2079 Baishakh Engineering Mathematics-1 Old is Gold Solution | Part-1 | Er. Brijkishor Jaiswal State Leibnitz’s theorem. If \( y = \log(x + \sqrt{a^2 + x^2}) \) then using the theorem show that \((a^2 + x^2)y_2 + xy_1 = 0\) and hence show that \((a^2 + x^2)y_{n+2} + (2n+1)xy_{n+1} + n^2 y_n = 0\).
Комментарии отсутствуют
Информация о видео
18 марта 2025 г. 17:39:36
01:07:16
Другие видео канала